Archive for agosto 2013
O Gato Zumbi de Schrödinger e o Colapso da Função de Onda
Escrever
sobre ciência, em especial a física, é uma tarefa dura,
mas quando nós abordamos assuntos que gostamos é prazeroso escrever
textos, infelizmente esse não é o caso de hoje para mim. Porém é
uma tarefa necessária. Dia 12 desse mês foi aniversário do Físico
Erwin Schrödinger, um dos pais da mecânica quântica e o
idealizador de um dos experimentos mentais mais famosos de todos os
tempos, o maldito gato zumbi dentro de uma caixa. Com seu aniversário
várias páginas resolveram usar imagens do “gato de schrödinger”
para divulgar a data, inclusive o google fez um doodle super legal.
Nos comentários das páginas e no meu perfil pessoal vi perguntas,
várias delas, e notei que uma grande parte das pessoas acredita que
o experimento do gato realmente aconteceu e que o foco é o
gato dentro da caixa, então nosso texto de hoje será sobre isso; O
que de fato é o Experimento do Gato de Schrödinger e o que é que causa o colapso da função de onda.
Imagine
que você está afim de um(a) garoto(a), mas vocês mal se conhecem e
mesmo assim você quer chamar ele(a) para sair. Então antes de
convidá-lo para sair você resolve utilizar suas habilidades
matemáticas para tentar calcular qual a probabilidade dele(a) dizer
“sim” e “não”. Como você conhece pouco sobre essa outra
pessoa, você acha mais prudente dizer que a chance de receber um
“sim” é de 50% e a chance de receber um “'não” é
igualmente de 50%. Ok, antes de você perguntar existem duas
respostas para sua pergunta “sim” e “não”, então vamos
dizer que você se encontra num “estado” de resposta “sim-não”,
ou seja, um estado de dúvida, pois ambas respostas são possíveis.
Então você resolve perguntar para a pessoa se ela quer ou não sair
com você e (ao menos nesse texto) ela responde “Sim”, então a
sua probabilidade de receber um “sim” é agora de 100% e a do
“não” é 0%. Inicialmente você estava no estado “sim-não”,
agora seu estado colapsou para apenas “sim”. Simples, não?!
A idéia
do experimento do gato de Schrödinger é quase a mesma coisa. De forma simplória, imagine que você coloca um gato dentro de uma caixa, a qual está
devidamente lacrada (mas tem ar suficiente para o gato ficar lá
dentro), junto ao gato tem um dispositivo macabro que, de forma
aleatória, pode ou não quebrar um frasco de veneno dentro da caixa
e matar o coitado do gato. Digamos que existe novamente 50% de chance
de o dispositivo quebrar o frasco de veneno e matar o gato, e 50% de
chance do dispositivo não quebrar o frasco e o gato continuar vivo.
Enquanto não abrirmos¹ a caixa e vermos se o gato está vivo ou
morto, sabemos apenas que ele tem 50% de chance de estar vivo e 50%
de chance de estar morto, dizemos então que ele está no estado
“vivo-morto”. Assim que abrimos essa caixa devemos encontrar ele
ou vivo ou morto, ou seja, ou ele estará 100% vivo e 0% morto ou 0%
vivo e 100% morto. Exatamente da mesma forma que aconteceu no exemplo
de você convidando uma pessoa para sair. Mas note que nesse caso "abrir" a caixa representa uma medida do sistema, uma medida do gato vivo ou morto e não que é um observador (uma pessoa) forçando o gato a assumir um estado específico, o observador pode e deve ser substituído por algum aparelho como trataremos isso de forma mais correta no final desse texto.
Agora
que você tem uma ideia do assunto, vamos formalizar um pouco e
espero que você tenha paciência e vontade de ler.
Muito
antes da mecânica quântica surgir, Thomas Young já mostrava, por
meio do famoso experimento da dupla fenda, que um elétron poderia se
comportar como uma onda. Em 1926, a partir de trabalhos publicados
por Einstein e Planck, o físico francês Luis deBroglie introduz a
idéia da onda de matéria, em que se podia demonstrar
matematicamente as propriedades ondulatórias da matéria, um elétron
por exemplo.
Uma vez
que para partículas subatômicas esse caráter ondulatório é muito
visível e importante, foi introduzida uma ferramenta matemática
chamada de função de onda ψ.
Essa função tem importância fundamental na mecânica quântica,
uma vez que ela serve para descrever as principais características
de sistemas quânticos, como a energia, momento, posição e como
eles se comportam.
Para se
obter essa função ψ de onda, basta se extrair soluções da famosa
equação de Schrödinger, por exemplo. É como o "encontre o x" da matemática do ensino médio, mas um pouco mais complicado.
 |
| Equação de Schrödinger. |
Como essa
partícula é muito pequena, seu estado é dado pela interpretação
estatística de Bhorn, sobre a função de onda, em que |ψ|²
é a probabilidade de se encontrar a partícula em um ponto x,
no instante t.
A probabilidade de se encontrar a partícula naquela região é a área do gráfico que está em vermelho. No gráfico acima é bastante provável encontrar a partícula em A e quase impossível em B. Mas vamos supor que conseguimos medir com exatidão a partícula no ponto C, dessa forma todas as medidas consecutivas deveriam ser iguais, fazendo nossa função de onda se tornar um pico em C, a isso damos o nome de colapso da função de onda.
Assim, vê-se que há dois tipos de processos físicos completamente distintos: Os “comuns” no qual a função de onda evolui lentamente regida pela equação de Schrödinger e as “medidas” em que ψ colapsa súbita e descontinuamente.
Esses
processos são importantes para mostrar o caráter ondulatório e
probabilístico da mecânica quântica. Além de que o processo do
colapso da função de onda é amplamente citado por indivíduos que
fazem uma abordagem mística/esotérica da mecânica quântica, que é
justamente o motivo pelo qual eu odeio escrever sobre esse assunto.
Nós não
conseguimos saber antes da medida, onde uma partícula se encontra,
podemos apenas conhecer a probabilidade dela ocupar certas regiões
do espaço, quando executamos uma medida e encontramos a partícula
dizemos que houve um colapso da função de onda, assim a função de
onda que conhecíamos antes já não existe mais, e a partícula
volta a evoluir no tempo a partir de novas condições iniciais. Isso
nos mostra a sensibilidade do sistema ao ser medido.
Pelo
caráter matemático da equação de Schrödinger, ela pode nos
prover várias soluções para a função de onda, ψ, ψ1, ψ2 e etc. Nós
podemos também somar duas dessas equações de onda e obter uma nova
função de onda, ψ=Aψ1 + Bψ2, A e B são
constantes. Quando fazemos essa soma, nós estamos sobrepondo dois
estados quânticos e é isso que nos interessa!
Cada uma
dessas funções de onda pode nos fornecer um valor diferente para
energia, por exemplo. Assim ao somar essas duas funções de ondas,
não obteremos mais apenas um valor para energia, mas sim dois. Dessa
forma a partícula regida pela soma dessas funções de onda pode ter
sua energia entre esses dois valores e não mais apenas um valor.
Mas como
entender isso fisicamente? Imagine que pegamos vários sistemas
quânticos exatamente idênticos, sem a superposição de estados,
quando medimos a energia em um desses sistemas ele nos dará a
energia E1 quando medirmos novamente a energia em qualquer outro
desses sistemas nos obteremos novamente E1. Quando temos a
superposição de estados quânticos, essa certeza desaparece. Ao
realizar a medida da energia no primeiro sistema quântico, podemos
obter E1 ou E2 quando fizermos a medida no segundo sistema,
novamente podemos ter E1 ou E2 e o mesmo ocorrerá na medida
de qualquer um dos outros sistemas identicamente preparados. E se
fizemos a medida em um primeiro sistema e obtivermos E1 nada
garante que a medida dos outros sistemas sejam também E1, pois
ainda existe a probabilidade de medir E2. Assim mesmo com sistemas
idênticos, podemos obter energias diferentes.
Com a
superposição, as medidas de propriedades dos sistemas passam a não
ser mais bem definidas, mas sim estatísticas. Enquanto nenhuma
medida é feita nós dizemos que os estados estão sobrepostos (ou
superpostos) e a única coisa que podemos fazer é calcular a
probabilidade de medir o sistema e encontrar um estado ou outro.
Foi nesse
sentido que surgiu o experimento mental do Gato de Schrödinger. Como
antes da medição não conseguimos saber em qual estado quântico
nosso sistema está, dizemos que ele está em uma superposição de
estados. Schrödinger trouxe esse fenômeno para um exemplo mais
palpável: Colocando um gato dentro de uma caixa junto a uma
armadilha que possa matá-lo, dizemos que o gato pode possuir dois
estados, vivo ou morto. Quando fechamos a caixa, não temos como
saber se a armadilha disparou e matou o gato, ou se a armadilha não
disparou e o gato continua vivo. A menos que a caixa seja aberta, nós
não poderíamos afirmar que o gato está vivo, nem que o gato está
morto, mas sim que ele ocupa uma superposição de estados, em que
existe uma probabilidade dele estar vivo e outra probabilidade dele
estar morto.
Agora
vamos ver como Schrödinger elaborou originalmente o experimento e
tentar tirar está besteira de que a consciência humana é quem
colapsa a função de onda.
Schrödinger
escreveu:
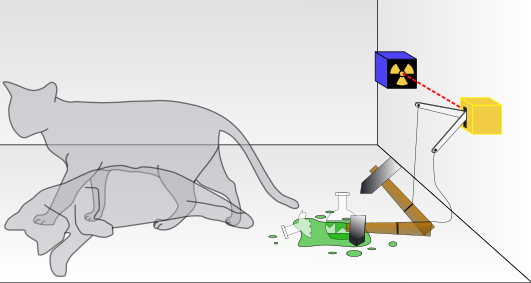
“Qualquer um pode mesmo montar casos bem ridículos. Um gato é trancado dentro de uma câmara de aço, juntamente com o dispositivo seguinte (que devemos preservar da interferência direta do gato): num tubo contador Geiger há uma pequena porção de substância radioativa, tão pequena que talvez, no decurso de uma hora, um dos seus átomos decaia, mas também, com igual probabilidade, talvez nenhum se decaia; se isso acontecer, o tubo contador liberta uma descarga e através de um relé solta um martelo que estilhaça um pequeno frasco com ácido cianídrico. Se deixarmos todo este sistema isolado durante uma hora, então diremos que o gato ainda vive, se nenhum átomo decaiu durante esse tempo. A função-Ψ do sistema como um todo iria expressar isto contendo em si mesma o gato vivo e o gato morto simultaneamente ou dispostos em partes iguais.”
No primeiro exemplo que dei lá no começo do texto sobre o experimento do gato de Schrödinger eu disse que você tinha que abrir a caixa para que o gato assumisse ou um estado vivo ou um estado morto, fiz isso apenas a título de simplificação, mas já aviso que isso é perigoso, pois pode dar interpretações erradas, para tanto fique muito atento as linhas abaixo!
Falamos em grande parte do texto sobre medições, mas o que afinal são essa medições? É consciência humana de quem realiza o experimento? NÃO! Na descrição correta do experimento mental que está aí acima, vemos que há uma fonte radiativa que pode emitir uma partícula ou não, que será registrada pelo contador Geiger. A medição é representada pelo disparo do contador Geiger ao registrar o evento da emissão da partícula e não a intervenção de um observador humano. O que chamamos de medição nesse caso é a interação entre o sistema microscópico e o macroscópico de forma a deixar um registro permanente, ou seja, é no momento que a mecânica quântica interage com a mecânica clássica. Pois o sistema macroscópico não pode ocupar uma superposição de estados da mesma forma que o sistema quântico. Alguns oportunistas gostam de pegar a palavra “medição” e dar um caráter totalmente humano e consciente a ela chamando-a de “observador”, quando na verdade não é! Heisenberg usava a palavra evento ao invés de medição, mas infelizmente a moda não pegou.
Para finalizar vejam esse vídeo e comparem com nossa explicação:
É isso pessoal, espero que tenha ficado claro para todo mundo que não tem nenhum gato de verdade dentro de nenhuma caixa, é tudo um experimento mental, no qual nosso interesse é apenas criar uma forma palpável de exemplificar a superposição de estados.
Algumas referências:
- Tales of Schrödinger's Cat
- Introdução a Mecânica Quântica - Griffiths
- Física em 12 Lições Fáceis e Não Tão Fáceis - Feynman
sexta-feira, 16 de agosto de 2013
Posted by
Thiago V. M. Guimarães
Campos e Partículas - A Nossa Visão Moderna do Universo
No texto passado
falamos sobre simetrias nas leis da física. Nesse texto de hoje
vamos tratar de uma leve introdução da relação entre partículas
e campos do ponto de vista da Teoria Quântica de Campos (TQC). No
próximo texto iremos relacionar os dois assuntos tratando da quebra
espontânea de simetria e, nesse contexto, falaremos sobre dois
mecanismo muito importantes, o de Goldstone e o de Higgs. Vou deixar
os planos a curto prazo em formato de lista para que você possa
acompanhar melhor:
1 – Simetrias
2 – Partículas e
Campos
3 – Quebra Espontânea
de Simetria.
4 – O que são
Partículas Elementares?
5 – O que é
Supersimetria?
Vamos ao que interessa.
No final do século
XIX, o Lorde Kelvin¹ disse que o céu estava limpo, exceto por duas
pequenas nuvens negras, se referindo a como estava a física da
época. O problema é que essas duas pequenas nuvens negras eram nada
mais do que a mecânica quântica e a teoria da relatividade. Em
pouco tempo, essas duas nuvens negras cresceram e deram origem a uma
enorme tempestade.
É justamente da junção
de parte dessas nuvens que vamos falar aqui, mas não vou me focar em
descrições de títulos, e sim dar explicações e depois atribuir
títulos a elas.
Uma coisa que é comum
de se ler por aí é sobre a incompatibilidade entre a mecânica
quântica e a teoria relatividade. Mas isso não é totalmente
verdade, existem vários pontos em que a mecânica quântica e a
relatividade se encaixam muito bem e é disso que se trata a TQC².
Desde a formulação de teorias modernas da física, os campos se
fizeram presente, como na teoria do eletromagnetismo de Maxwell, por
exemplo. Então veio Einstein, Minkowski, Lorentz, Poincaré e deram
a física clássica uma nova abordagem, a abordagem relativística,
que deu formas diferentes a nossa visão dos campos. A essa nova
visão sobre os campos nós chamamos hoje de Teoria Clássica de
Campos. Com a inserção da mecânica quântica nesse contexto, ou
seja, com a quantização desses campos, obtivemos uma teoria bem
abrangente e que mete o bedelho desde a cosmologia até a física da
matéria condensada, que é a Teoria Quântica de Campos.
Mas qual a graça da TQC?
Essa teoria foi
postulada pela primeira vez no final de 1920 e desenvolvida ao longo
das décadas seguintes. E uma das principais coisas que a TQC fez,
foi mudar nossa visão de mundo. Pois essa teoria nos fez ver um
universo todo permeado por campos, que dão origem as partículas que
formam nosso universo, colocando os campos em uma posição
fundamental para compreendermos a natureza. Mas para ficar mais fácil
nossa compreensão, para começar, vamos pensar apenas em elétrons.
Em todo o universo, há
um campo chamado de “campo de elétrons”, que é um campo
fermiônico que citamos no texto sobre Matéria e Energia. Um elétron
propriamente dito não é um campo, mas sim uma vibração localizada
em um campo. Na verdade, cada elétron no universo é uma vibração
localizada em um único campo.
Os elétrons não são
as únicas partículas que consistem em vibrações localizadas de um
campo, na verdade todas as partículas são. Por exemplo, há um
campo de fótons, um campo de quark up, um campo de glúons, um campo
de múon, ou seja, há um campo para cada partícula conhecida. E,
para todos eles, uma partícula é apenas uma vibração localizada
do campo.
Esse é o caso também
do bóson de Higgs. O campo de Higgs interage com as partículas
fornecendo a sua massa, mas é difícil observar este campo
diretamente. Por esse motivo temos que fornecer energia para esse
campo, através de colisões de partículas, para lhe causar
vibrações que são detectadas como partículas, no caso, o bóson
de Higgs. Então, observar uma partícula em acelerador, por exemplo,
é nada mais do criar e observar vibrações em determinados campos.
Essa idéia dá uma
visão completamente diferente de como o mundo subatômico funciona.
Pois existe uma grande variedade de diferentes campos permeando todos
os lugares e o que nós pensamos que é uma partícula, na realidade
é simplesmente uma vibração do campo ao qual ela é associada.
Isto tem consequências
importantes sobre a forma como pensamos sobre como as partículas
interagem. Por exemplo, considere um processo simples, onde dois
elétrons são disparados um contra o outro e são espalhados. Na
visão semi-clássica de dispersão, um elétron emite um fóton e
depois recua. O fóton viaja para o outro elétron, que o “recebe”
e também recua. Isto é como ter duas pessoas em cima de dois skates
e um deles joga uma bola para o outro: o skate da pessoa que
arremessa a bola se move para trás em resposta à massa da bola,
assim como o skate da pessoa que apanha a bola.
Na TQC,
uma vibração no campo do elétron provoca uma vibração no campo
dos fótons. A vibração no campo do fóton transporta energia e
momento para outra vibração no campo do elétron e é absorvida.
No famoso processo em
que um fóton se converte em um elétron e um anti-elétron, as
vibrações do campo dos fótons são transferidas para o campo do
elétron e dois conjuntos de vibrações são configurados – um dos
quais está de acordo com a vibração do elétron e o outro de
acordo com a vibração do anti-elétron³.
Essa abordagem de campos e
vibrações explica como o universo funciona em um nível profundo e
fundamental. Estes campos abrangem todo o espaço. Alguns campos
podem interagir com outros campos, enquanto que outros podem parecer
inertes. O campo fóton pode interagir com os campos de partículas
carregadas, mas não pode interagir com os campos dos glúons ou dos
neutrinos. Por outro lado, um fóton pode interagir indiretamente com
o campo do glúon, em primeiro lugar, fazendo vibrações nos quarks
que, em seguida, fazem os glúons vibrar.
Campos quânticos são
realmente uma forma bem diferente de ver o universo. Tudo, e eu quero
dizer TUDO mesmo, é apenas uma consequência da vibração de muitos
campos infinitamente grandes. O universo inteiro é feito por esses
campos e essa coisa dá um grande nó na nossa cabeça.
No próximo texto, nós
vamos tratar de como essas partículas “aparecem” na quebra
espontânea de simetria nesse campos. Iremos falar um pouco sobre o
mecanismo de Goldstone, em que partículas perdem sua massa e o
mecanismo de Higgs, no qual partículas ganham massa. Caso você
queira acompanhar bem o próximo texto aconselho que você dê uma
estudada em “energia potencial” pode ser por material de ensino
médio, ou por esse texto.
1 - Em The London, Edinburgh and Dublin Philosophical Magazine and Journal of Science, Series 6, volume 2, page 1 (1901) "Nineteenth-Century Clouds over the Dynamical Theory of Heat and Light."
2 - Note que o ponto problemático da junção entre Mecânica Quântica e Relatividade se dá no campo gravitacional, quando tentamos quantizar esse campos surgem infinitos na nossa teoria que estragam a nossa brincadeira.
Veja mais:
- Lectures on Physics - Feynman (o física em 12 lições também serve)
- Introduction to Quantum Field Theory. John Cardy
quarta-feira, 14 de agosto de 2013
Posted by
Thiago V. M. Guimarães
Tag :
Aniquilação
,
Antipartículas
,
Bóson
,
Campos
,
divulgação Científica
,
Energia
,
Férmion
,
Matéria
,
Teoria Quântica de Campos
A Bela Simetria do Universo
Dando
continuidade ao nossos textos sobre física, em especial física de
partículas que campos. Hoje vamos tratar de um assunto muito
importante para os físicos da minha área; Simetria. Sem esse tema não conseguimos tratar quase nada da física moderna que vocês tanto gostam de ler!
Simetria
é algo totalmente presente em seu dia a dia, pois ela está contida
em nosso corpo, em praticamente todos os outros animais, em grande
parte dos objetos e formas geométricas. Por exemplo, na imagem a
baixo vemos 2 formas simétricas e uma antissimétrica. Na primeira
forma, se rotacionamos a tulipa em 1/8 de circulo ela ficará
exatamente da mesma forma. Já a ervilha apresenta uma simetria
diferente, se rotacionarmos ela, ela não parecerá simétrica, porém
podemos notar que um dos lados é exatamente igual ao outro. Na
terceira imagem, flor da cana-da-índia, não existe simetria de
nenhuma forma. Podemos ainda pegar uma esfera, que é uma forma
geométrica totalmente simétrica, não importa se você a gire, ou a
translade, ou a espelhe, ela sempre irá parecer igual.
Nosso
cérebro também tende a buscar simetria nas coisas e a achar beleza¹
nisso. Assim, nada mais natural que buscar simetrias nas leis do
nosso universo. Todas essas definições de simetria, de harmonia, de
estética, também existe na física. Mas o que elas são exatamente?
Bem, esse
assunto agora pode ser abordado de três formas, a primeira é bem
simples e intuitiva, a segunda vai exigir de você conhecimento
razoável de física, vetores e geometria (abordei isso aqui) e a
terceira forma é a para físicos experientes, obviamente aqui
abordaremos a primeira forma.
Para nós,
equações simétricas são aquelas que depois de sofrerem uma certa
transformação (rotação, translação) permanecem iguais, ou seja,
sem alterar seu significado. Um exemplo simples é uma soma de
números positivos, 2 + 3 = 5, podemos trocar a ordem a ordem e obter
a mesma reposta, 3 + 2 = 5, assim existe uma certa simetria na
adição. Porém o mesmo não vale para a subtração, pois 2 – 3 =
-1 e 3 – 2 = 1.
Apesar do
exemplo simples, simetrias muitas vezes são complexas e têm um
impacto profundo na física. E para entendermos um pouco do assunto
temos que falar de uma GRANDE mulher, Emmy Noether. Ela se tornou a
mulher mais influente da matemática em uma época que as mulheres
eram proibidas de frequentar determinadas universidades (veja um
pouco da história dela aqui). Mas o que ela fez e porque isso é
tão importante?
Antes de
Noether, os cientistas já tinham notado que certas coisas, como a
energia elétrica e carga, eram "conservadas". Ou seja, a
quantidade de energia de um sistema é o mesma antes e depois de um
evento, como uma colisão por exemplo. Da mesma forma, a carga
elétrica pode se movimentar, mas a carga total permanece a mesma.
(Note que isso só funciona em sistemas "fechados", que não
estão ganhando ou perdendo energia ou cargas de uma fonte externa).
Mas ninguém compreendia exatamente por que essas coisas eram
conversadas, é aí que entra o trabalho de Noether.
| Noether |
O que ela
fez, a grosso modo, foi conectar essas leis de conservação com
simetrias matemáticas que podem ser expressas como equações. Wow,
isso foi simplesmente genial, pois o que ela fez foi mostrar que cada
simetria implicava em uma quantidade física conservada. Por exemplo,
se uma equação não foi alterada quando você a mudou de um ponto a
outro no tempo, significa que a energia foi conservada. Se você a
mudou entre um ponto a outro espaço e ela continua inalterada, então
seu momento linear foi conservado. Assim conseguiu-se explicar as
leis de conservação como a manifestação mensurável de simetrias
nas leis que regem o universo.
O teorema
de Noether levou a uma apreciação mais profunda do papel da
simetria nas leis que regem o universo. Agora, a simetria de uma
teoria particular, é uma das primeiras coisas que os físicos
consideram quando se avalia uma teoria.
Para um
físico a simetria tem valor estético e isso tem importância impar
quando “julgamos” nossas teorias. Sim, a beleza importa! Agora
toda vez que você olhar e se encantar com a beleza simétrica de
algo, lembre-se que esse também é o ponto de vista de beleza do
nosso universo.
Para o próximo texto,
tentarei tratar algo também muito importante, a quebra espontânea
de simetria. Porém eu ainda não faço idéia de como abordar isso
sem matemática, também não achei nenhum texto que tenha tentado.
Então é bem provável que demore um pouco para eu ter tempo de
escrever esse texto.
Referências:
Referência Base: Symmetry: How Beautiful Math Makes Elegant PhysicsLeitura complementar: Física em 12 lições, Fáceis e não Tão Fáceis - Feynman
quarta-feira, 7 de agosto de 2013
Posted by
Thiago V. M. Guimarães
Matéria e Energia - Energia escura, Matéria escura e a Massa do Fóton (pt 3)
Esse é o nosso último
texto da série Matéria e Energia, Aqui vamos abordar um pouco de
cosmologia e tratar também da relação entre o fóton e a famosa
E=mc².
Quando você pega um
texto ou um artigo de Cosmologia é comum ouvir falar de matéria,
radiação, matéria e energia escura. Então vamos começar esse
texto com alguns esclarecimentos sobre como esses assuntos são
tratados na cosmologia
Matéria X Antimatéria:
Um dos maiores interesses dos cosmólogos nesse assunto é tratar a
diferença de quantidade entre matéria e antimatéria no universo.
Pois no nosso universo a matéria ordinária existe em bem maior
quantidade que a antimatéria, embora sempre vejamos matéria e
antimatéria serem produzidas aos pares, esse é ainda um dos grandes
mistérios da cosmologia.
Matéria X Radiação:
No início o universo era um lugar muito quente e com o passar do
tempo ele foi se expandindo e esfriando, até que hoje sua
temperatura é de 2,7K. Podemos entender o universo em seu princípio
e evolução como sendo um gás, ou um plasma, de partículas em uma
determinada temperatura. Se nós medirmos a energia cinética média dessas
partículas nesses sistemas, iremos encontrar o valor kT, em que
k é a constante de Boltzmann e T é a temperatura. Nesse contexto, a
matéria é qualquer partícula que sua energia de repouso (mc²) é
grande em relação a energia cinética média das partículas (kT),
assim, a velocidade dessas partículas é bem menor que a velocidade
da luz. Por sua vez, radiação é qualquer partícula que sua massa
de repouso é muito pequena quando comparada da kT e,
consequentemente, sua velocidade é bem próxima a da luz.
Resumindo esse ponto, temos:
Resumindo esse ponto, temos:
se mc² > kT → partícula de matéria com velocidade menor que a da luz.
se mc² < kT → radiação com velocidade igual ou próxima a da luz.
Talvez não tenha
ficado tão claro para você, mas o que acabamos de definir mostra
que o que é ou não matéria depende da temperatura do nosso sistema
e, considerando que ele resfrie com o tempo, depende também do
tempo. Com isso, logo no início do universo, quando a temperatura
era de milhões de milhões de graus, o elétron
era considerado como radiação pelos cosmólogos. Hoje, com o
universo muito mais frio, o elétron está na categoria de matéria.
No universo atual, pelo menos dois dos três tipos de neutrinos são
matéria, ou talvez os três tipos, por esta definição, mas todos
os neutrinos foram radiação no início do universo. Fótons sempre
foram e sempre serão radiação, uma vez que eles não têm massa.
O que é a matéria escura?
Podemos dizer a partir
do estudo dos movimentos das estrelas e de outras técnicas que a
maior parte da massa de uma galáxia vem de algo que não brilha, mas que interage apenas gravitacionalmente, esse algo é o que chamamos de matéria escura. Um enorme trabalho foi feito para provar que as partículas
conhecidas, que se comportam de maneira comum, não podem ser
responsáveis por essa estranha massa e para explicar este efeito,
várias especulações foram propostas e muitas delas se mostraram erradas, através da observação de como as galáxias se parecem e se
comportam. Das especulações sobreviventes, um dos
principais candidatos é que a matéria escura é formada de
partículas pesadas e desconhecidas. Mas nós não sabemos quase nada
sobre elas. Experimentos em breve poderão nos trazer novos
conhecimentos, mas obviamente não temos garantia disso.
E energia escura?
Foi descoberto
recentemente que o universo está se expandindo cada vez mais rápido,
e provavelmente a responsável por isso é o que chamamos de "energia
escura", mas, infelizmente, essa “energia” não é realmente
energia. Como Sean Carroll gosta de dizer, essa “energia” é na verdade uma combinação
de pressão e densidade de energia. Então, por que as pessoas chamam
de "energia"? Parte do problema vem das relações públicas. Da
mesma forma que “partícula de Deus”, “energia escura” parece
um nome legal; já “tensão escura” soa estranho. É basicamente uma estratégia de marketing jornalístico e de certa forma isso é inofensivo, já que os cientistas
sabem exatamente o que se quer dizer por “energia escura”. Mas se
você realmente quer entender o que está acontecendo, é importante
saber que a energia escura não é uma forma escura de energia, mas
sim algo mais sutil. Além disso, como a energia, a energia escura
não é um objeto ou um conjunto de objetos, mas uma propriedade que
os campos ou combinações de campos, ou espaço-tempo em si podem
ter. Nós ainda não sabemos o que é o responsável pela de energia
escura, cuja presença podemos inferir a partir da aceleração do
universo, mas assim com a matéria escura, esperamos que com o tempo o assunto fique mais claro tanto para todos nós.
Uma das principais
coisas que você deve ter notado nessa série de textos é que nós
físicos somos péssimos com palavras e nem um pouco criativo para
criar nomes, eu mesmo já tive uns 3 cachorros com o nome de
“cachorro”, então não é nada surpreendente nomes como “Big
Bang”, “Buraco Negro” entre outros. Somo péssimos com isso e
geralmente a mídia se aproveita para disseminar nomes que chamam a
atenção. Mas nos perdoem.
Como falamos de
energia, matéria, massa, fótons e outros assuntos, acho prudente
encerrar essa série tratando de algo que estou cansado de ler:
“E=mc² diz que o fóton tem massa”. NÃO, isso não é verdade!
Vou tentar explicar com
um pouco de calma, pois vamos ter que usar matemática aqui
(quebrando a promessa de não usar matemática nesse blog). Apesar de
E=mc² ser uma das equações mais conhecidas da ciência, ela não
está na forma completa, pois ela não considera partículas sem
massa. A forma completa da famosa equação é na verdade:
E²=m²c⁴+p²c²
em que E é a energia
do corpo, m é a massa de repouso, c é a velocidade da luz, p é o
momento linear do corpo. Quando o corpo está parado, p é zero, e
caímos na famosa E=mc², quando m=0, como é o caso do fóton, temos
E=pc. Ou seja, partículas sem massa tem automaticamente velocidade c (elas nunca estão paradas).
Aí você, que é um
cara inteligente e aprendeu bem o conteúdo do ensino médio, vai
dizer; “mas momento não é a relação entre massa e velocidade
(mv)?”. Sim você está certo, mas para ondas eletromagnéticas o
momento é dado pela constante de Planck (h) dividida pelo comprimento de onda (λ). Assim o fóton tem energia sem precisar ter massa.
Então, quando em uma
discussão alguém argumentar que o fóton tem massa devido a
“E=mc²”, saiba que está errado, pois essa equação não vale
para partículas sem massa, para esse caso o correto é “E=pc”,
que pode ser simplificado para “E=hf”, em que f é a frequência
do fóton.
Resumindo, temos 3 casos diferentes para a energia:
Partículas com massa em repouso:
E=mc²
Partículas com massa em movimento:
E²=m²c⁴+p²c²
Partículas sem massa (sempre em movimento):
E=pc
Mas a história da
massa do fóton não é um assunto tão simples, que espero abordar
em outra oportunidade, mas deixo aqui alguns pontos em aberto para
tentar atiçar a curiosidade de vocês; nós afirmamos que o fóton
tem massa zero, mas nós até hoje só conseguimos calcular um limite
superior para sua massa, não um inferior. Então, isso é suficiente
para afirmar que o fóton não tem massa? Algumas outras teorias
confirmam que o fóton não tem massa? Existem teorias de fótons
massivos? Se fótons tivessem massa aconteceria algo com a teoria da
relatividade?
Pense sobre essas
questões, espero abordá-las em um outro texto em breve.
Aqui encerramos nossa
série de 3 textos sobre Matéria e Energia, espero que tenha sido
útil para alguém e que tenha deixado vocês com dúvidas e vontade
de pesquisar mais.
Lembrando que esses
textos foram baseados nos textos do professor Matt Strassler, o qual
eu traduzi, adaptei, acrescentei, retirei, melhorei (ou piorei).
Então se você tiver domínio do inglês vá no blog dele e veja os
textos nos quais me baseei para escrever esses aqui, têm coisas excelentes lá!